Team members: Chaves, B. D., Comaty, S., Mootian, G., Shen, Y., Suehr, Q., Zlatanovic, L.
Problem Statement
Measles is caused by a virus known simply as the measles virus and is spread mainly through droplet contact. Measles virus is one of the most highly transmissible pathogenic microorganisms known to humankind, according to Young and Rall. It is estimated that 30 to 40 million cases of measles cases occur annually worldwide, resulting in about 400,000 deaths per year (Cowan). Despite the enormous progress made in deciphering the basis of measles virus pathogenesis and in the creation of effective attenuated vaccines, how the virus causes disease, including rare, but serious, central nervous system (CNS) complications, remains poorly understood. Furthermore, little is known about its routes of transmission and its survival in the environment (Young and Rall). Measles is also known as rubeola and should not be confused with the maculopapular rash disease rubella (Cowan, 2010).
Widespread vaccination has made measles in the United States nearly unheard of, with only a few cases reported per year (Cowan, 2010). A recent outbreak of measles linked to one or more Disney theme parks has reinvigorated discussion of measles vaccination. By April 10, 2015, 131 confirmed measles cases were reported in the outbreak in California, with 40 cases in California having traveled to the parks in December. An additional 16 cases linked to this outbreak have been reported elsewhere in the U.S., in six other states by April 10, 2015, for a total of 147 illnesses. In Quebec, a total of 158 cases of the same genotype (B3) were reported in a non-immunizing religious community by March 28, and the importation to Canada was linked to travel to Disneyland. Cases from this outbreak also were observed in Mexico. This outbreak, larger than those typically seen in recent years in North America, may raise questions regarding the continuing success of measles control and its routes of transmission (Clemmons et al.; Worden et al.). The objective of this case study is to model the transmission effect of measles in the theme park outbreak.
Hazard Identification
The Measles Virus
Measles virus is a member of the Paramyxoviridae family, within the Morbillivirus genus. Its genome consists of approximately 16,000 bases of non-segmented, single-stranded negative-sense RNA, meaning that the viral genome is transcribed immediately upon entry into the cell. Virions are spherical and enveloped and the envelope is derived from the host cell as the viral particle buds from the plasma membrane (Kayser et al, 2005; Young and Rall). No other organism is responsible for measles except the measles virus (Kayser et al, 2005). Similar viruses within the Morbillivirus family are capable of causing disease in other animals, such as dogs, cats, cattle, seals, dolphins, and turtles (Kayser et al, 2005). Non-human primates can also be a host, and measles is a threat to their conservation. However, the overall population is estimated to be too low to maintain transmission (Public Health Agency of Canada (PHAC)).
Infection, pathogenesis and development of disease
The pathogenesis of measles has not been fully explained. It is assumed that the virus, following primary replication in lymphoid tissues, is distributed hematogenously in two episodes (Kayser et al., 2005). The virus implants in the respiratory mucosa and infects the tracheal and bronchial cells. From there it travels to the lymphatic system, where it multiplies and enters the bloodstream (Cowan, 2010). Viremia carries the virus to the skin and to various organs. The measles virus induces the cell membranes of adjacent host cells to fuse into large syncytia, giant cells with many nuclei. These cells no longer perform their proper function. The virus seems proficient at disabling many aspects of the host immune response, especially cell-mediated immunity and delayed-type hypersensitivity (Cowan, 2010). The host may be left vulnerable for many weeks after infection. This immune response disruption is one of the reasons that secondary bacterial infections with Streptococcus spp. and Haemophilus influenzae are so common (Cowan, 2010).
This first viremic phase carries the virus throughout the body and seeds it in organs such as the liver, spleen and bone marrow. After a further round of multiplication, a second viremic phase will deposit the virus in organs throughout the body (Cowan, 2010). The second viremia may be the release of large numbers of virus into the bloodstream or the movement of virus within the cells of the immune system. At this stage, disease becomes apparent with the patient showing typical signs and symptoms: sore throat, dry cough, headache, conjunctivitis, lymphadenitis, and fever (as high as 40.5 °C/105°F) (Cowan, 2010). In a short time, unusual oral lesions called Koplik’s spots appear as a prelude to the characteristic red maculopapular exanthem that erupts on the head and then progresses to the trunk and extremities until most of the body is covered. The rash gradually coalesces into red patches that fade to brown. The rashes seen with measles appear following the second viremia (Cowan, 2010). The exact cause of the viral rashes varies. Some rashes represent virus-infected cells being destroyed by the immune response, whereas others represent blood vessel damage due to virus (Hardy, 2002).
The measles virus incubates in the host for 10 to 12 days (range of 7 to 21 days) and causes systemic infections, reflecting rounds of viral replication in more than one organ of the body. The important feature of this process is the long incubation period during which the patient becomes infectious but shows no clinical disease (Hardy, 2002; PHAC). The acute measles infections rely on rapid multiplication of the virus in order to manufacture and shed new viral particles before the host has had time to elicit a neutralizing immune response (Perry and Halsey, 2004). Persons with measles are usually considered infectious from four days before until four days after onset of rash with the rash onset being considered as day zero (Perry and Halsey, 2004).
Complications and sequelae
In a small number of cases, children develop laryngitis, bronchopneumonia, and bacterial secondary infections. In a small percentage of cases, the virus can cause pneumonia. Affected patients are very ill and often have a characteristic dusky skin color from lack of oxygen (Perry and Halsey, 2004). Occasionally (1 in 100 cases), measles progresses to encephalitis and may result in various CNS changes from disorientation to coma. Permanent brain damage or epilepsy can occur. The most serious complication is called subacute sclerosing pan-encephalitis (SSPE), a progressive neurological degeneration of the cerebral cortex, white matter, and brain stem. Its incidence is approximately one case in a million measles infections and it afflicts primarily male children and adolescents. The disease generally develops 7 to 10 years after infection. This disease involves loss of memory and personality changes, and usually results in death within six to 12 months of the onset. The risk of developing SSPE may be higher when measles occurs prior to the second year of life (Perry and Halsey, 2004).
Although the immunological response elicited by most infected, immunocompetent individuals is sufficient to clear the virus and provide life-long protection, a period of transient immune-suppression is a notorious characteristic of measles virus infection and is likely the basis of most of the complications and the subsequent fatalities following acute infection (Young and Rall). Measles during pregnancy has been associated with spontaneous miscarriage and low-birthweight babies, but severe birth defects have not been reported (Cowan, 2010).
Active Immunity
A person who has had measles once will not suffer from measles a second time and is thus called immune. However, such specific or acquired immune mechanisms do not represent the only factors that determine resistance to infection. Live vaccines are used to protect against measles (Kayser et al., 2005). The MMR vaccine (measles, mumps and rubella) contains a mixture of live attenuated viruses of the three agents and is administered through injection (Plotkin et al., 1965). The MMR vaccine is a sterile lyophilized preparation of (1) a measles virus derived from Enders' attenuated Edmonston strain and propagated in chick embryo cell culture, (2) a strain of mumps virus propagated in chick embryo cell culture, and (3) the Wistar RA 27/3 strain of live attenuated rubella virus propagated in WI-38 human diploid lung fibroblasts. The growth medium for the viruses is a buffered saline solution containing vitamins, amino acids, sugars, fetal bovine serum, human albumin, and neomycin among other ingredients. The reconstituted vaccine is for subcutaneous administration. Each 0.5 mL dose contains not less than 1,000 TCID50 (tissue culture infectious dose) of measles virus; 12,500 TCID50 of mumps virus; and 1,000 TCID50 of rubella virus (Plotkin et al., 1965; Plotkin et al., 1967).
Like any other drug the vaccine does have side effects. They include allergic reactions, reddening of the skin, itching of the feet or hands, swelling of the eyes and face and unusual tiredness or weakness (CDC).
Exposure Assessment
Measles is one of the most contagious infectious diseases, transmitted principally by large respiratory droplets. Transmission is mostly horizontal. Epidemic spread is favored by crowding, low levels of herd immunity, malnutrition, and inadequate medical care. There is no reservoir other than humans, and a person is infectious during the period of incubation, prodrome phase, and the skin rash but usually not during convalescence. Only relatively large, dense populations of susceptible individuals can sustain the continuous chain necessary for transmission (Hardy, 2002).
Transmission routes
Direct contact is the primary mode of transmission, whereas airborne droplet and indirect contact are less common (PHAC). The number of times people touch their faces with their hands is enough to almost guarantee that virus in the nose or saliva will be transferred to the hands and from there to other individual and environmental surfaces (Hardy, 2002). Airborne transmission via aerosolized droplet nuclei has been documented in closed areas (e.g., office examination room) for up to 2 hours after a person with measles occupied the area (CDC).
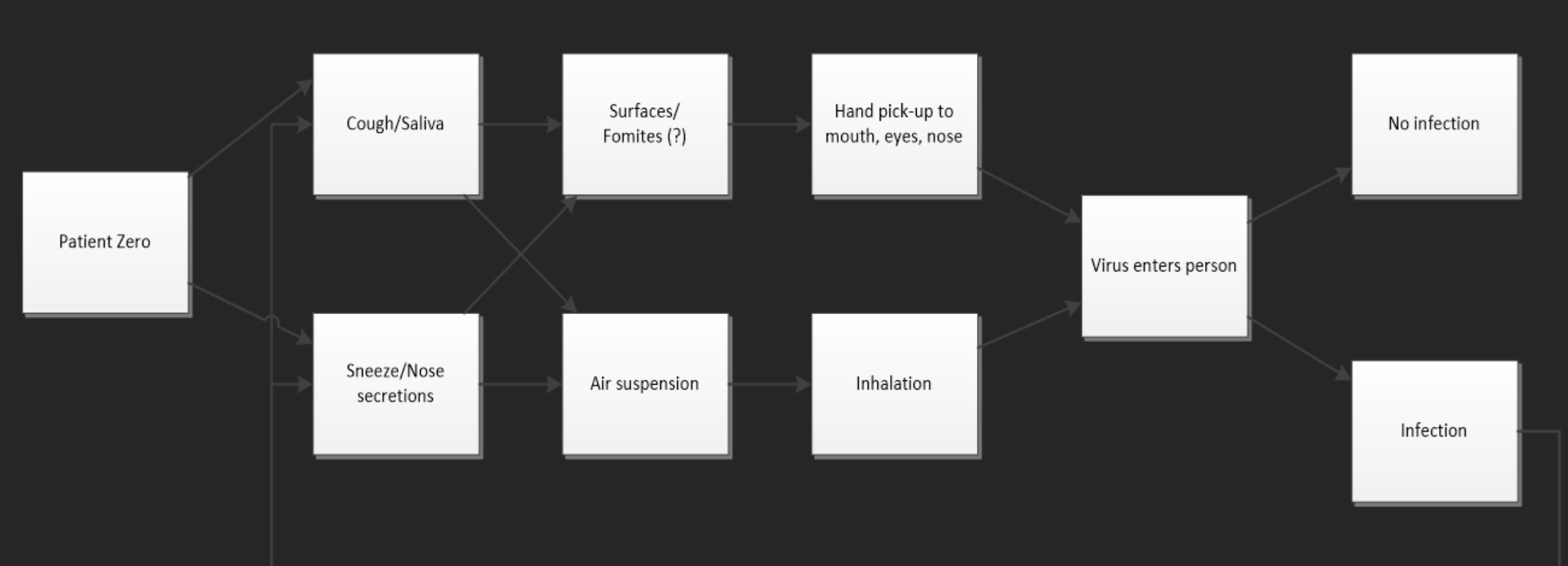
The most likely routes of transmission for the virus are depicted in Fig. 1.The role of airborne droplets has been documented as a vehicle for measles transmission although the concentration of the virus in the air is not known. Recently, fomites have been suggested as a potential way of infection although very limited data exist on the survival of the virus on inanimate surfaces.
Fig. 1. Most likely routes of transmission of the measles virus
Disease transmission
Classic infectious diseases such as measles can be modeled assuming that the infection is transmitted randomly between infectious and susceptible people. The rate of transmission will be proportional to the product of the number of susceptibles multiplied by the number of infectious people (Hardy, 2002). Mathematically, the proportional rate of increase means that there must be a constant that moderates the product (β). That constant represents the probability of effective transmission. The more infectious people (I) or susceptibles (S) there are, the greater the rate of new infections occurring (N) (Hardy, 2002).
\begin{align*} N = \beta*S*I (1) \end{align*}
The number of people directly infected by someone who is infected by a particular microorganism in an entirely susceptible population is termed Ro, the basic reproductive rate (Hardy, 2002). Assuming that the infected and susceptibles can mix randomly and homogenously, the mass action principle can be used to define Ro as the product of the susceptibles (S), the probability of effective transmission (β) and the period of time each case is infectious (D) (Hardy, 2002).
\begin{align*} R_o= S*\beta*D (2) \end{align*}
Highly infectious diseases like measles have high values of Ro, typically between 10 and 20, whereas poorly infectious diseases such as leprosy have Ro values much closer to 1(Hardy, 2002). The outcome of a proposed measles epidemic can therefore be predicted to some extent. The key parameters in an epidemic are the size of the population and the rate of new susceptibles appearing (Hardy, 2002). The epidemic will fade and disappear as R falls to less than unity, but if the population density is high enough the organism may persist and reappear later as a second epidemic (Hardy, 2002).
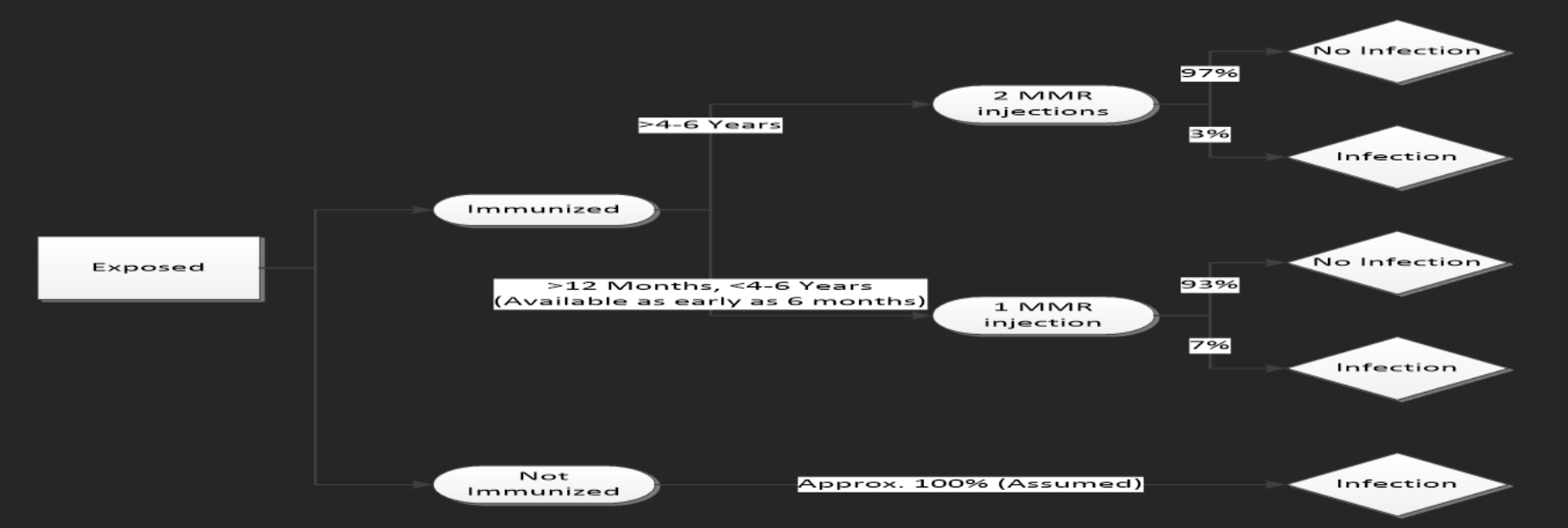
The outcome of exposure to the measles virus will depend largely and significantly on immunization status of the individual (CDC). Fig. 2 shows the reported probabilities of infection for unimmunized subjects as well as for those who have received one and two doses of the MMR vaccine.
Fig. 2. Measles infection probability tree
Exposure to measles at a theme park scenario
Crystal Ball® was used to estimate the total number of people exposed to measles at the theme park where the outbreak occurred. It was assumed that if a susceptible individual was exposed, he or she would develop the disease. Thirty-nine cases of measles were directly attributed to exposure at the theme park (Zipprich et al.). The total number of people exposed at the theme park was estimated as:
\begin{align*} Total\ Exposed = Observerd\ Cases / Susceptible \end{align*}
The susceptible fraction was estimated as:
\begin{align*} Susceptible\ Fraction=unvaccinated\ fraction+ineffectivly\ vaccinated fraction \end{align*}
or
\begin{align*} Susceptible\ Fraction=(1-vaccination\ coverage\ rate)+(1-vaccine\ effectiveness\ rate)*vaccination\ coverage\ rate (4) \end{align*}
Transmission model for the theme park measles outbreak
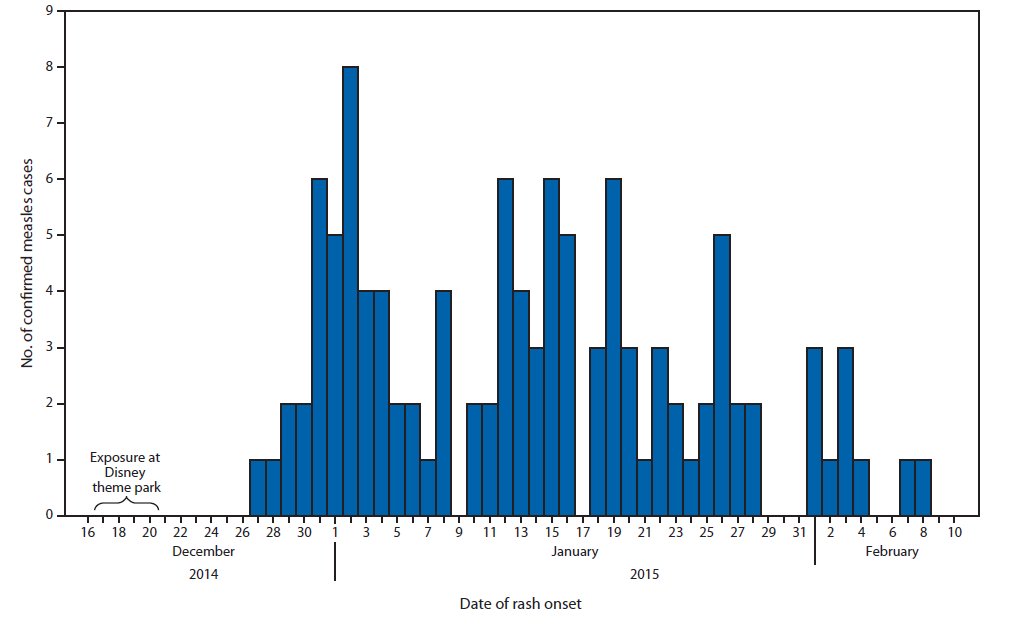
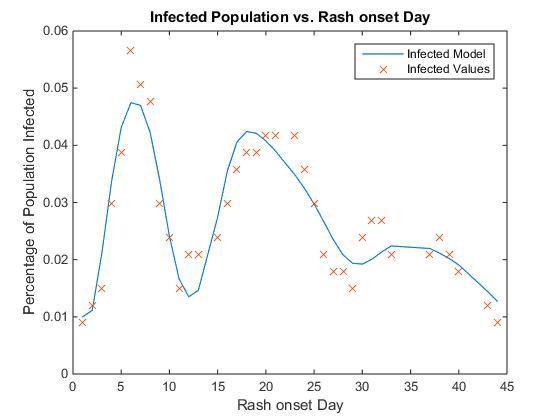
An SEIR model was developed to model the transmission effect of measles in the theme park outbreak. The model considers the short term effects of the measles epidemic and how it spread through the environment based on interactions and biological properties. Using data from the CDC and the California Department of Public Health (CDPH), the outbreak reports for the epidemiologically linked measles cases were collected over 55 days after the initial infection period at the theme park (Fig. 3). The histogram indicates the linkage between the exposures of the population at the theme park, with a distinct rash onset time, and multimodal peaks of the outbreak periodically throughout the epidemic. These multimodal peaks are prevalent in historical measles cases and have a strong biological association based on the infectious period of the patients, showing that there is a period during which people are significantly more contagious.
Fig. 3 Number of confirmed measles cases in California based on the day of rash onset reported. Indicating the distinct lag time of rash onset and multimodal characteristics of the outbreak (Zipprich et al.)
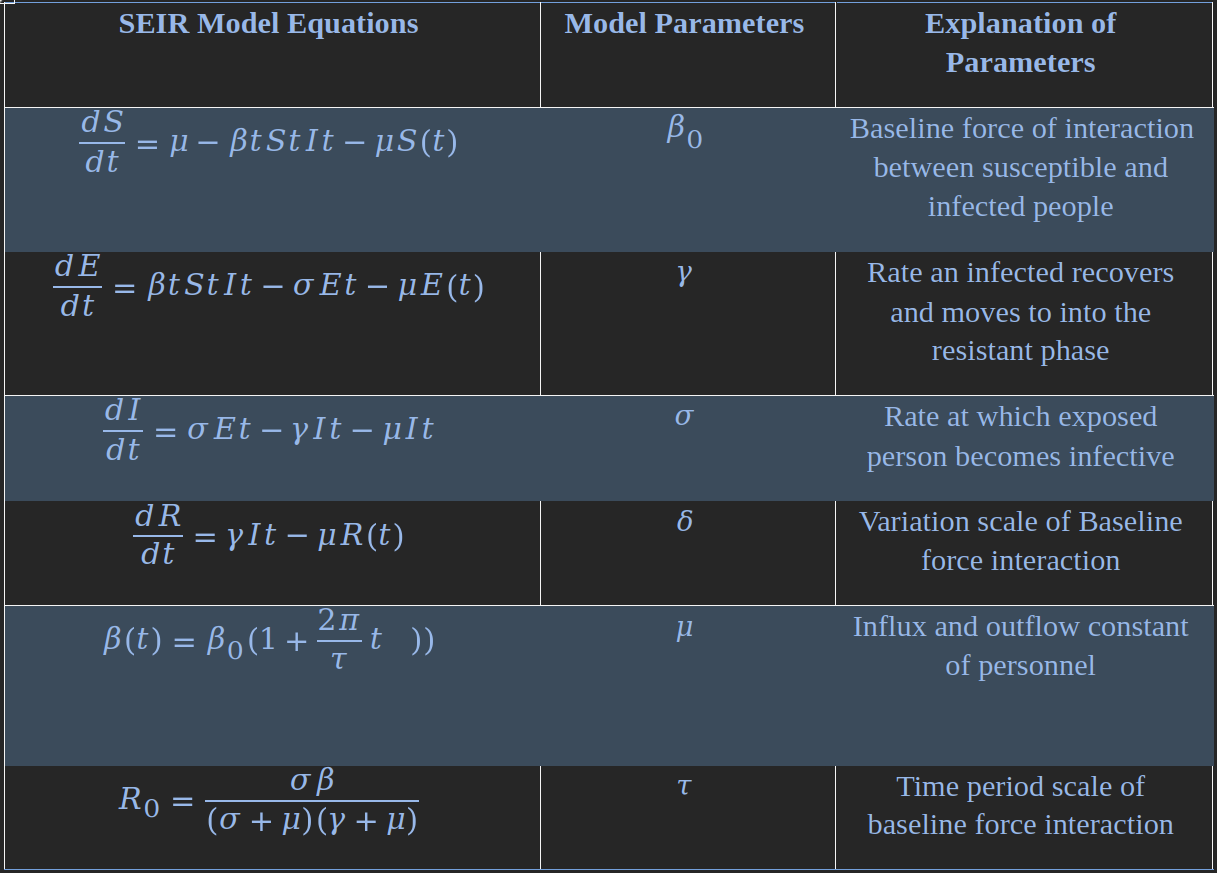
The biological properties of measles and historical reports of short term reported cases were used to develop an outline of the model parameters and initial conditions for the SEIR model. A few constraints to the model were made due to limitations of data and simplicity of assumptions, such as only considering outbreaks within the state of California, assuming that there is a constant state of influx and outflow of the population (keeping the total amount of people in the system constant), and the force of infection varies as a function of time and measles infectious periods. The linked differential equations of the SEIR Model are shown in Table 1.
Table 1. List of inputs and outputs of the SEIR mathematical model
The SEIR model shows the unique characteristics of the epidemic nature of a measles outbreak; however, the parameters must be fit to each individual case of an outbreak assuring that the model parameters are physically realistic. Using the moving average of the theme park outbreak in December 2014, the model was fit to the data and optimized in order to provide the most accurate mathematical description of the outbreak, as shown below.
Dose Response
The infectious dose of the measles virus is estimated to be 0.2 units by intranasal spray (PHAC). However, it is not known how many viral particles are needed to cause disease. Therefore, it is not possible to develop a dose-response model for measles infection. It is presumed that everyone who comes in direct contact with the virus will become infected if not adequately immunized or if they had not had the disease previously.
Risk Characterization
The SEIR model fits the reported case data well with an RMSE of 0.0043% and 36 degrees of freedom (DOF), showing that it is a good mathematical representation of the outbreak with physically realistic parameters (Fig. 4). In addition, the basic reproductive number R0 based upon the equation in Table 1 shows a reasonable value of 14.1638, where reported reproductive numbers of measles have been shown to be on the range of 12-20 (CDC).
Fig. 4. Infected population (as a percentage vs reported rash onset day) and the fitted model equation based on the theme park data.
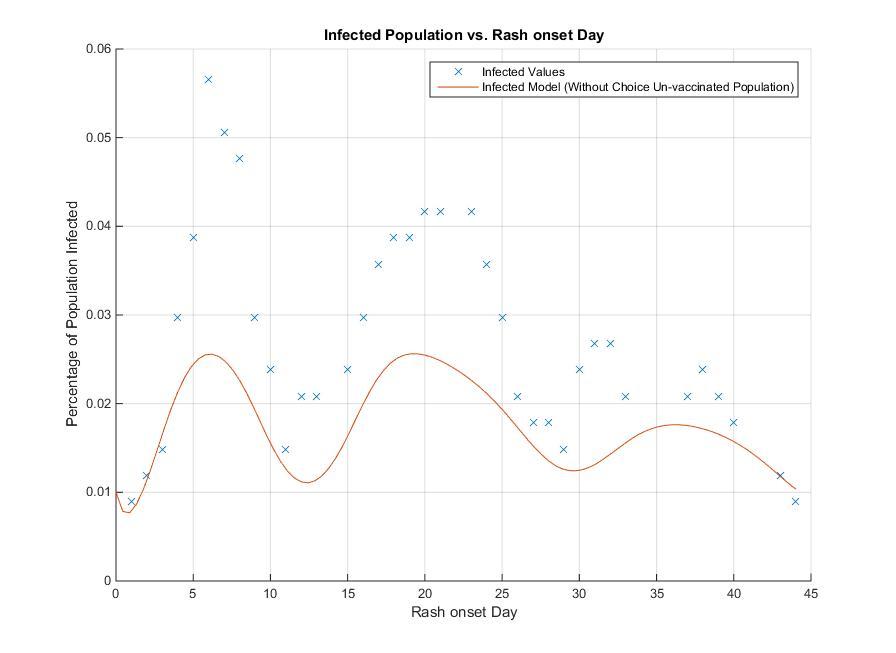
The objective of building the model of theme park outbreaks is to mathematically demonstrate the effects of vaccination on population susceptibility to measles infection with the ultimate goal of increasing herd immunity. The ability to reduce the susceptible population before an epidemic occurs is the safest way to reduce the spreading of disease. For the theme park outbreak, 42% of the population that got measles was unvaccinated due to philosophical or religious reasons. If we model the same outbreak, subtracting this 42% of the population that would have otherwise had a reduced susceptibility to measles, we can observe the reduction in the outbreak mechanics throughout the days after the infection (Fig. 5).
Fig. 5. Comparison of infected model (without choice un-vaccinated population) to actual infected values of the theme park outbreak incident.
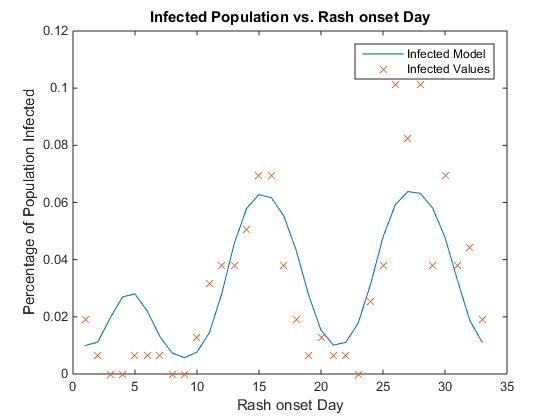
SEIR model validation In addition to modelling the California theme park outbreak, the credibility of the model on other reports was investigated, further demonstrating the robustness of the model built for this case study. Reports of an outbreak in an American ship traveling the Australia in 1882 named the ‘Roslin Castle’ provided detailed investigations on the percentage of susceptible population in a confined environment, and the number of measles cases over the period of the voyage by days (Paterson et al., 2013). In addition, the report demonstrates a multimodal peak as seen in the theme park outbreak report, showing that it is a prevalent phenomenon in the biological mechanics of measles. Although the outbreak was given before 1882, the results indicate that based upon the total number of passengers that became sick relative to the total population the immune population to measles was at ~81-97%.
Fig. 6. Infected population (as a percentage vs reported rash onset day and the fitted model equation based on the Roslin Castle.
With an RMSE of 0.0172% and 32 DOF, the SEIR model fits the Roslin Castle measles outbreak well, demonstrating similar parameter values, with physically realistic results (Fig. 6). The reproductive number of the Roslin Castle outbreak was shown to be R0 = 13.466 similar to previous reports of measles Reproductive number.
With the ability to mathematically fit an SEIR model to measles outbreaks at a day by day resolution, more intriguing insights into the transmission modelling of an epidemically associated virus can be discovered, such as the mechanics of the multimodal peaks and how certain preventative and reactionary measures can be taken place to reduce the spread and risk of populations from further extending an outbreak.
Risk Management & Communication
Vaccination
Vaccination is the most efficient and cost effective way to prevent the spread of measles. Nationwide, MMR vaccination coverage data obtained from the CDC shows that between 1995 and 2014, about a 90% of children 19-35 months and 13-17 year old were vaccinated. Whereas vaccination coverage among 19-35 months and 13-17 year olds has been successful (~90%), the coverage rates should be increased and sustained. Vaccination campaigns should be directed to the < 13 months group to increase vaccinations coverage rates to 96 to 99% hopefully by 2020 (CDC). This will help preserve herd immunity and prevent future outbreaks.
Transmission in high density settings
Since theme parks are overcrowded settings that have a potential for widespread transmission, infants below 6 months of age should not be taken there because currently they have no options for vaccination. Children 6 to 12 months of age (not covered under the standard vaccination schedule) should be vaccinated if they will be taken to the theme parks, similar to the CDC international travel guidelines. In addition, in daycare centers, schools and educational institutions, vaccination should be offered for those that are not up to date with age appropriate vaccination (first dose to the unvaccinated, second dose to those with one documented dose). Persons who continue to be exempted from or who refuse measles vaccination should be excluded from the school, daycare, or other institutions until 21 days after the rash onset in the last case of measles. Persons who work in close contact settings including healthcare facilities are at a high risk of exposure to measles and at an increased risk of transmission to persons at high risk of severe illness. These individuals should have presumptive evidence of immunity to measles to prevent any potential outbreaks.
Importation of measles into the United States
Some of the measles outbreaks reported by CDC have been traced back to imported measles from infected visitors coming to the United States (indirectly imported) and US citizens acquiring the virus outside US and bringing it back to the country. In 2004 the number of cases linked to direct importation of the virus were higher than indirect importation. Usually foreign students who come to the US on F-1 visas are required to provide an up-to-date immunization card before enrollment. A similar measure for tourists coming to the US should be considered, especially if visitors come from countries where measles is endemic, a reemerging problem or has low vaccination coverage rates. Tourists from these nations should be required to produce a valid immunization card during their visa application.
For US citizens travelling to countries where measles is endemic, the government could consider a requirement for vaccination to prevent non-vaccinated individuals from bringing back the virus into the US. According to the CDC, a total of 1053 measles cases had been reported from 01/01/2000 to 01/31/2012 within the United States. Of the 1053 reported cases, 420 cases (~40%) were internationally imported and 633 cases (~60%) were indigenous. The distribution of the reported measles cases varied considerably among the 9 areas in the United States, with the largest numbers of cases reported in the Pacific States (28%).
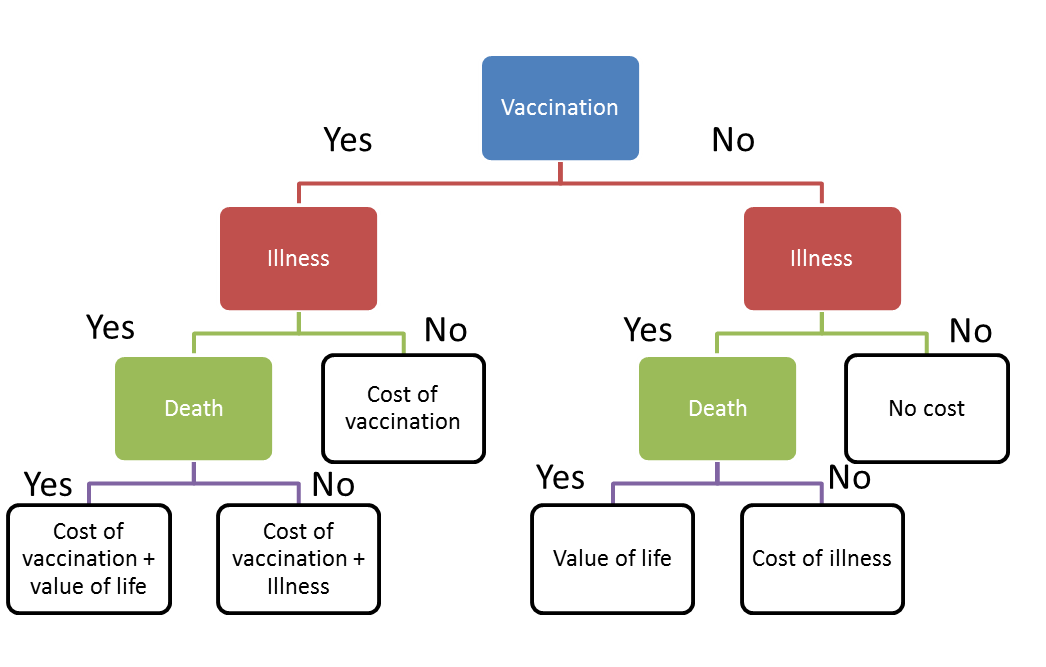
Decision tree for vaccination cost analysis
The possible consequences and corresponding cost of measles vaccination, illnesses, and disease were evaluated with a decision tree analysis. The structure of the decision tree is shown in Fig. 7. Here we assume that death and illness can be evaluated by cost. Then the expected cost of vaccination and non-vaccination could be calculated with the following equations:
\begin{align*} Estimated\ cost\ of\ vaccination = P_I \times(1-P_E)[(C_L+C_V)\times P_M + (C_V+C_I)(1-P_M)]+(1-P_I)\times C_V \times P_E (5) \end{align*}
\begin{align*} Expected\ cost\ of\ non\ vaccination = P_I[C_L \times P_M + (1-P_M) \times C_I] \end{align*}
The goal of building a decision tree is to compare the final cost of vaccination and non-vaccination in the event of disease. However, the illness probability (PI) is an unknown parameter and it will vary based on the exposure situations. Therefore, we set a threshold value of illness probability. When we need to make the decision under a certain situation, we can compare the threshold illness probability value to the estimated illness probability corresponding to that specific situation.
To get a threshold of illness probability, we assume that the expected final cost of vaccination and non-vaccination is equal and then calculate the threshold illness probability based on equation 5. Then if the real illness probability is greater than the threshold, the final cost of vaccination will be lower than the final cost of non-vaccination. If the real illness probability is greater than the threshold, vaccination will lead to a higher cost than non-vaccination then non-vaccination would be a cheaper choice.
\begin{align*} Threshold\ P_I = \frac{-C_V}{(1-P_E)[(C_L+C_V)\times P_M + (C_V+C_I)(1-P_M)]-C_V \times P_E - [C_L \times P_M + (1-P_M) \times C_I]} \end{align*}
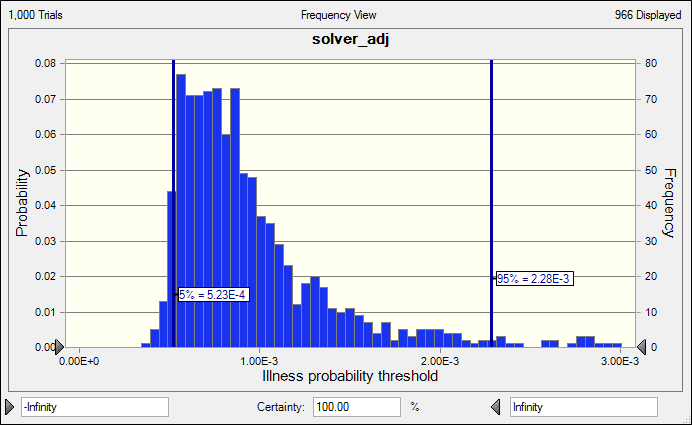
Since it is hard to get an accurate evaluation of illness and death cost, Crystal Ball® was used to estimate a possible threshold value distribution (Fig. 8). As a result, the illness threshold value ranged from 0.5~2.3×10-3. The median threshold value is 8×10-4. In the case of the Disneyland measles outbreak, we assume that 20,000 people visited the park the day that the outbreak initiated, of which 2,000 were unvaccinated. Among these 2,000 persons who did not take vaccine, there are 20 illness cases. Then the ratio of infection is around 20/2000=1.0× 10-2. This ratio is much larger than 8× 10-4, which would lead to higher cost of non-vaccination than cost of vaccination. Therefore, in the case of visiting Disneyland, taking vaccination is a cost effective choice.
Fig 7. Structure of decision tree
Fig. 8. Crystal ball calculation results for illness probability threshold
Risk communication
Education and awareness will be key to reducing measles outbreaks. Social, electronic and print media should be leveraged to raise awareness about the adverse health consequences of lack of vaccination. The media campaigns should also focus on discrediting negative and scientifically unsubstantiated false claims on the association of measles vaccine with developmental disorders. A renewed emphasis should be given to effective communication and public engagement with parents, health professionals, community leaders and the media, to gain their trust, understand and address vaccine concerns and support vaccine acceptance.
Communication strategies should address culture and belief systems and aim for dialogue and engagement with communities against vaccinations rather than one-way communication. A communication plan should encompass the following points.
• Advocacy should begin with decision-makers, including political leaders, health-care professionals, teachers and other educators, religious leaders, women’s, youth, labor, business and professional associations and other influential groups — to explain the benefits of immunization, address community concerns and invite their active participation in the program.
• Communication surveillance should be done to catch any emerging community concerns about vaccination and to take appropriate measures to address them.
• Data collection, analysis and mathematical modeling to determine the challenges, evidence-based messages, strategies and channels for community engagement.
• Consider health programs to support children of low-income families to get vaccinated.
Of particular relevance related to the California outbreak described in this case study is the current trend of certain affluent communities to decline vaccination for their children. The decline in vaccination rates in that particular state compared to the national overall trends may have contributed to the high number of cases in the Disneyland measles outbreak and its spread through the state of California, making it increasingly important to better communicate risk and improve community awareness on the dangers of the measles virus.